• 인공 신경망
• 활성화 함수
• 손실 함수
  • 회귀(Regression)
  • 분류(Classification)

인공 신경망

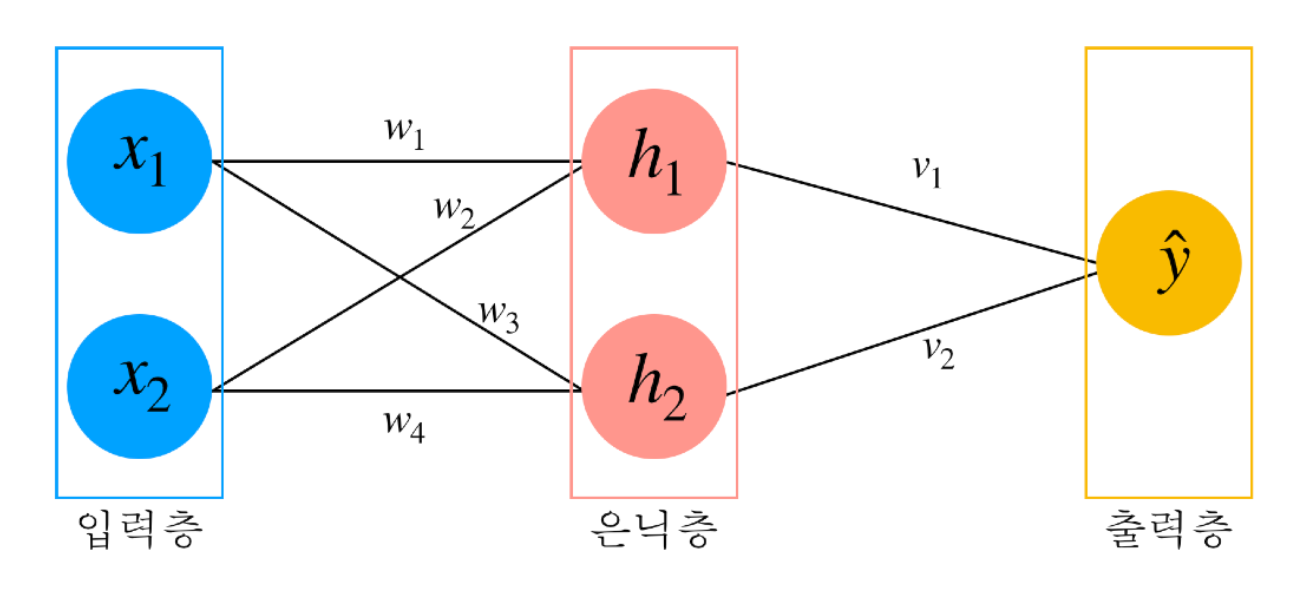
• 가중치: 입력층부터 출력층까지 연산을 할때 각 층 사이에 있는 연산을 위한 값
  ex) \(w_1\), \(w_2\), \(v_1\)

• 출력 수식:

\[h_1 = w_1x_1 + w_2x_2 + b_1, h_2 = w_3x_1 + w_4x_2 + b_2\] \[\hat{y} = v_1h_1 + v_2h_2 + b_3\]

활성화 함수

• 선형(linear) 함수
  그대로 값을 보내주는 항등함수

\[\mathbf{a}(x) = x\]

• 시그모이드(sigmoid) 함수
  각 층의 관계를 비선형적으로 변환하며 모든 입력값에 대해 과 1 사이 값으로 변환

\[\mathbf{\sigma}(x) = {1\over 1 + e^{-x}}\]

• tanh 함수
  시그모이드 함수와 유사하지만 -1과 1 사이의 값으로 취하며 0부근에서 더 가파른 기울기를 갖는다는 차이점이 있음

\[\mathbf{a}(x) = tanh(x)\]

• ReLU(Rectified Linear Unit) 함수
  0보다 작을 때는 0 반환, 0보다 클 때는 그대로 값을 반환. 두 개의 직선을 이어 만든 것으로 비선형 함수지만 선형과 매우 유사

\[ReLU(x) = max(0, x)\]

• Leaky ReLU 함수
  ReLU 함수의 변형된 식으로 마이너스 값도 취할 수 있는 함수

\[\mathbf{a}(x) = \begin{cases} -x\quad (x > 0)\\ \alpha x\quad (x\leq0)\end{cases} \quad, \alpha는\; 상수\]

• ELU(Exponential Linear Unit) 함수
  Leaky ReLU보다 부드러운 함수로 0보다 작은 영역에서 직선을 지수로 바꿔 곡선으로 만든 함수

\[\mathbf{a}(x) = \begin{cases} -x\quad (x > 0)\\ \alpha(e^x - 1)\quad (x\leq0)\end{cases} \quad, \alpha는 \;상수\]

• 소프트맥스(softmax) 함수
  모든 Output 값들이 0과 1 사이 값이 반환되고 모든 성분의 합은 항상 1. 각 성분을 확률처럼 사용이 가능

\[softmax(\mathbf{x}) = {e^{\mathbf{x}} \over \sum_{k=1}^n e^xk} \quad (e는 \;자연상수)\]

손실 함수

손실 함수를 이해하려면 지도 학습을 알아야한다.

지도 학습이란 모델이 학습하는 과정에서 정답을 알려주는 것으로 예측이 얼마나 정확한지를 판단하는 데 판단하는 그 척도가 바로 손실 함수

1. 회귀(Regression)
   원하는 결과값이 연속적인 변수인 것을 예측하는 문제

2. 분류(Classification) 원하는 결과값이 클래스라는 유한한 모임으로 분류되는 문제

회귀(Regression)

• 평균 절대 오차(Mean Absolute Error, MAE)
  예측값(\(\hat{y}\))과 실제값(\(y\))의 수직 거리의 평균으로 표현된 오차

\[L(\mathbf{y}, \mathbf{\hat{y}}) = {1 \over n}\sum_{i=1}^n \vert \hat{y}_i - y_i \vert\]

• 평균 제곱 오차(Mean Square Error, MSE)
  예측값(\( \hat{y} \))과 실제값(\(y\))의 수직 거리의 제곱의 평균으로 표현된 오차

\[L(\mathbf{y}, \mathbf{\hat{y}}) = {1 \over n}\sum_{i=1}^n (\hat{y}_i - y_i)^2\]

• 평균 제곱근 오차(Root Mean Square Error, RMSE)
  MSE 단위는 제곱된 결과를 주기 때문에 같은 단위로 만들어 주기 위해 제곱근을 씌운 손실 함수

\[L(\mathbf{y}, \mathbf{\hat{y}}) = \sqrt{ {1 \over n}\sum_{i=1}^n (\hat{y}_i - y_i)^2}\]

분류(Classification)

• 내적(inner product)
  \(a\), \(b\)를 벡터라고 하면 내적은 각 성분 곱의 합

\[a \cdot b = a_1b_1 + a_2b_2 + ... \;+ a_nb_n\]

• 교차 엔트로피 함수(cross entropy function)
  분류 문제를 위한 대표적인 손실 함수

\[L(\mathbf{y}, \mathbf{\hat{y}}) = -{1 \over n}\sum_{i=1}^n \mathbf{y}_i \cdot log(softmax(\mathbf{\hat{y}})) \quad(log는 \;자연로그)\]

• 이진 교차 엔트로피 함수(binary cross entropy function)
  이진 분류는 두 가지 상황을 분류하는 문제로서 원-핫 벡터로 표현하지 않아도 되기 때문에 예측 단계에서 소프트맥스를 사용하지 않고 일반적으로 시그모이드를 사용

\[L(\mathbf{y}, \mathbf{\hat{y}}) = -{1 \over n}\sum_{i=1}^ny_ilog(\hat{y}) + (1 - y_i)log(1 - \hat{y}_i) \quad(log는 \;자연로그)\]

[참조] 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기

끝!