• 하강법
• 경사 하강법
• 확률적 경사 하강법과 최적화 기법
• 기울기 사라짐
• 손실함수와 최적화

하강법

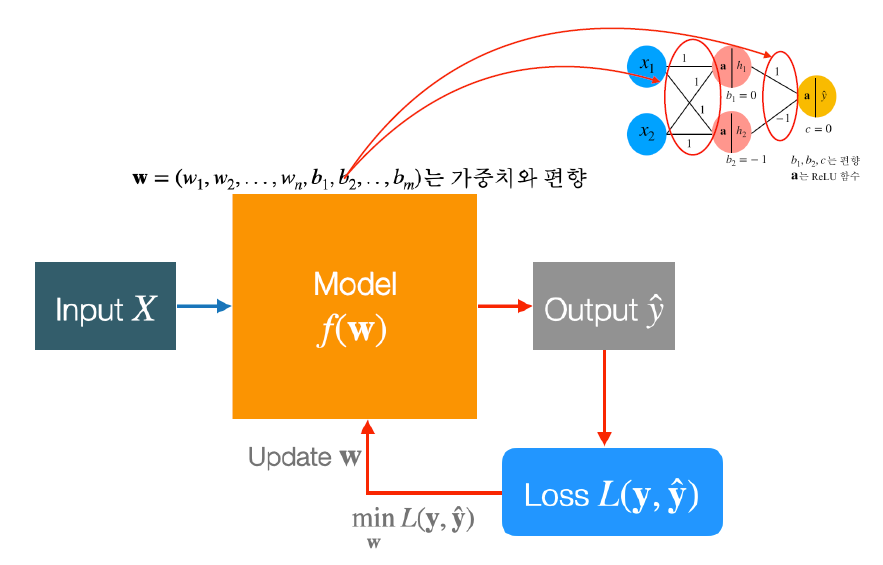
• 모델의 input을 받아 output을 추출하는 것을 예측이라고 함
• Loss Function은 실제 값과 예측 값의 차이를 나타내는 척도이며 차이가 작을 수록 학습이 잘 되고 있다는 것
• 목표는 그림에서 Loss 값을 작게 만드는 \(\mathbf{w}\)를 찾는 것

따라서 \(minL(y, \hat{y})\)을 목적 함수라고 칭함

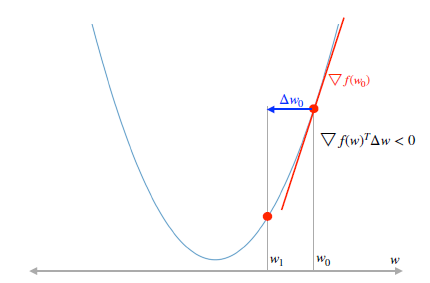
하강법이란 원래 지점보다 더 낮은 \(\mathbf{w}\)를 찾는 방법을 의미. \(\mathbf{w}\) 지점이 내려가는 방향과 접선의 기울기는 항상 반대이기 때문에 다음 부등호를 만족하면 됨

\[\nabla f(w)^T\Delta w < 0\]

• 초기 위치에 따라서 도착 지점이 달라질 수 있다는 단점이 있음
  ex) 3, 4차 그래프

경사 하강법

식 유도

\(w \;\leftarrow w \; + \; \mu \Delta w, \; \nabla f(w)^T\Delta w < 0\)
\(\Delta w \; = \; -\nabla f(w)\)
\(\nabla f(w)^T(-\nabla f(w)) \; = \; -\nabla f(w)^T \nabla f(w) \; < \; 0\)
\(w\;\leftarrow \; w \; - \mu \nabla f(w)\)

경사 하강법 적용

\(\mu = 0.4\) 대입

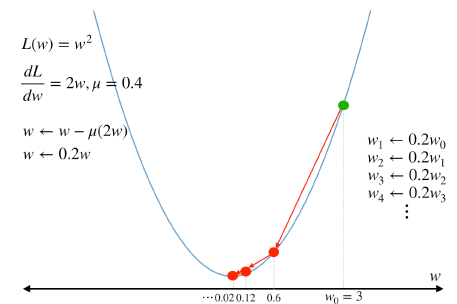
\(\mu = 0.6\) 대입

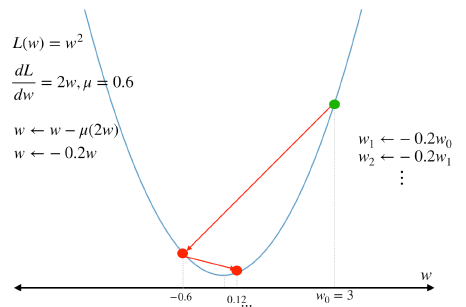
\(\mu = 1.2\) 대입

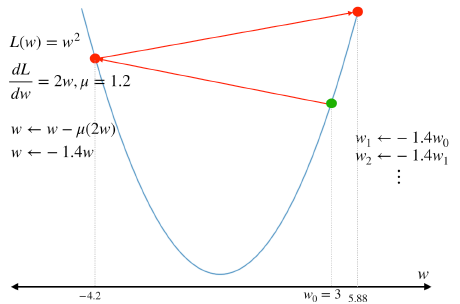
위 그림들 처럼 \(\mu\) 값이 너무 크면 수렴하지 않을 수 있고 \(\mu\) 값이 너무 작으면 수렴 속도가 너무 오래 걸릴 수 있기 때문에 적절한 \(\mu\) 값을 찾아야 한다.

확률적 경사 하강법과 최적화 기법

SGD(Stochastic Gradient Descent)

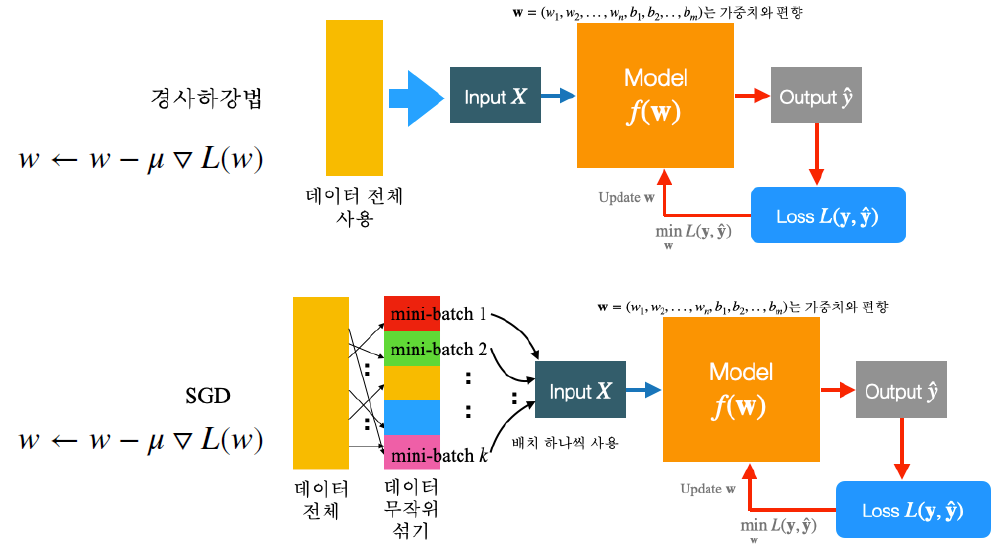
경사 하강법에서는 데이터가 엄청 큰 상황에서 알고리즘에 문제가 없더라도 하드웨어적인 문제로 동작이 잘 안되는 이슈가 있을 수 있다. 이를 보완해서 나온 것이 바로 SGD

• 데이터 전체를 입력 값으로 넣는게 아니라 데이터를 쪼개서 무작위로 mini-batch 형태로 하나씩 넣어줌
• 공식은 기존 경사 하강법과 동일

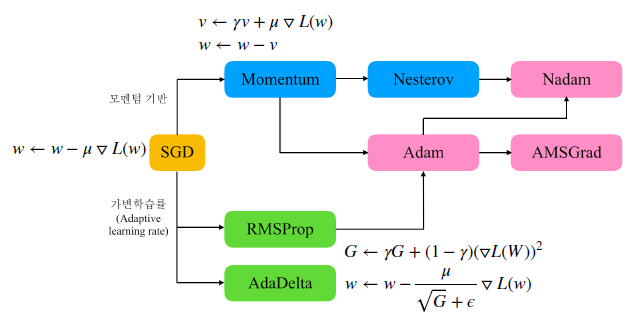
\(\mu\)(학습률)은 고정된 상수이기 때문에 상황에 따른 조절을 줄 수가 없어 해결하기 위한 다음과 같은 방법들이 있다.

1. 모멘텀 기반: 공식 뒤에 추가적인 값을 가해주는 것
2. 가변 학습률: \(\mu\) 값을 특정 규칙에 따라 바꾸어 주는 것

자주 쓰이는 Adam은 모멘텀 기반과 가변 학습률을 동시에 적용한 기법으로 볼 수 있다.

기울기 사라짐

인공신경망은 합성함수의 형태로 계산이 되어 그 미분은 연쇄 법칙을 통해 계산이 된다.

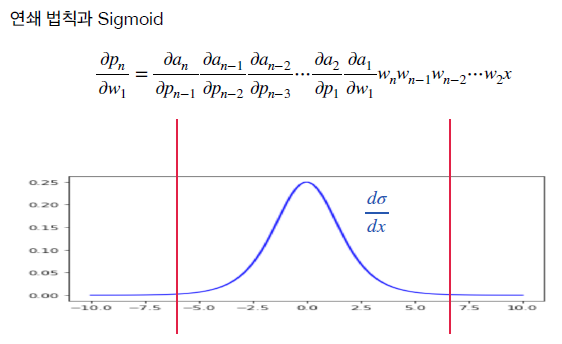
• Sigmoid 함수는 미분 값들을 곱할수록 0에 가까워짐

\({\partial p_n \over \partial w_1} \to 0\) 수식처럼 0에 가까워 지게 되면 \(w_1 \gets w_1 - \alpha {\partial p_n \over \partial w_1}\) 수식에서 미분값이 0으로 수렴하게 되어 가중치(\(w1\))가 업데이트 되지 않는 현상이 발생한다.

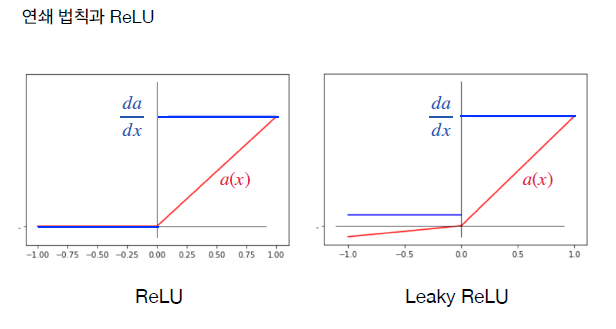
• ReLu 또는 Leaky ReLU 함수를 이용하면 방지 가능
• ReLU: 그래프 기준 0 이상의 값에 대해 미분값이 0이 되는 것을 방지
• Leaky ReLU: 그래프 기준 모든 값에 대해 미분값이 0이 되는 것을 방지

손실함수와 최적화

그림에서 보는 것과 같이 손실 함수의 종류는 다음과 같다.

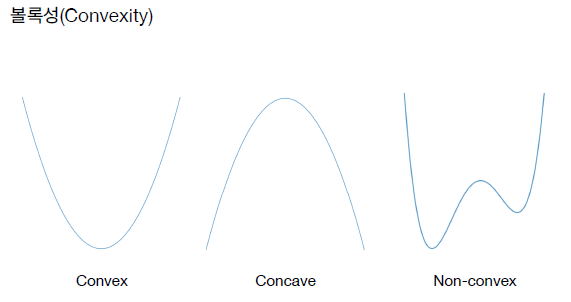
• Convex: 최소값을 찾기 가장 좋은 형태
• Concave: 최대값을 구하는 경우 좋은 형태이며 -를 곱해주면 Convex로 변환도 가능
• Non-convex:최소값을 찾기가 어렵기 때문에 되도록 Convex 형태로 만들어 주는 것이 좋음
• 둥글지 않더라도 직선 형태나 뾰족한 형태도 조건만 만족하면 Convex 형태로 볼 수 있음
• 조건: 그래프 상에 어떤 두 점을 잡아 잇더라도 그래프가 아래에 있는 경우

볼록성(Convexity)

• 함수 \(f\)가 concave면 \(-f\)는 convex다
• 함수 \(f, g\)가 convex이고 \(a, b \ge 0\)dlaus \(af + bg\)도 convex이다
• 모든 norm은 convex이다
• 함수 \(f, g\)가 convex이고 \(g\)가 일변수 증가함수라면 \(g(f(x))\)는 convex이다.

[참조] 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기

끝!